已知等差数列{an}的首项为a，公差为b，等比数列{bn}的首项为b，

问题解答题

已知等差数列{a_n}的首项为a，公差为b，等比数列{b_n}的首项为b，公比为a，n=1，2，…，其中a，b均为正整数，且b₂=6，a₃=8，a＜b．

（1）求a，b的值；

（2）数列对于{a_n}，{b_n}，存在关系式a_m+1=b_n，试求a₁+a₂+…+a_m．

答案

解：（1）由题设a_n=a+（n﹣1）b，b_n=ba^n﹣1，

∵b₂=6，a₃=8，

∴ab=6，a+2b=8，

∴或，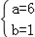

∵a＜b，

∴

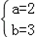
（2）由（1）数列{a_n}的通项公式为a_n=2+（n﹣1）×3=3n﹣1，

数列{b_n}的通项公式为b_n=3·2^n﹣1．

由a_m+1=b_n，得出3m=3·2^n﹣1，m=2^n﹣1．

∴a₁+a₂+…+a_m=（3×1﹣1+3×2﹣1+3×3﹣1）+…+（3×2^n﹣1﹣1）=

=3·2^2n﹣3+2^n﹣2．