问题
解答题
抛物线的顶点在原点，以x轴为对称轴，过焦点且垂直于对称轴的弦长为8，求抛物线的方程．
答案
解：设抛物线方程y2=2ax(a ≠0) ，则其焦点为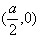
，
将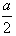
代入y2=2ax得y=±a，
∴2|a|=8，a=±4，
所求抛物线的方程为y2=±8x.
搜题请搜索小程序“爱下问搜题”
抛物线的顶点在原点，以x轴为对称轴，过焦点且垂直于对称轴的弦长为8，求抛物线的方程．
解：设抛物线方程y2=2ax(a ≠0) ，则其焦点为，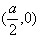
将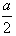代入y2=2ax得y=±a，
∴2|a|=8，a=±4，
所求抛物线的方程为y2=±8x.