问题
解答题
已知数列{an}的前n项和Sn=2n2+2n,数列{bn}的前n项和Tn=2-bn,
(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)设cn=an2·bn,证明:当且仅当n≥3时,cn+1<cn。
答案
解:(1)由于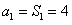 ;
;
当n≥2时,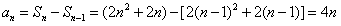 ,
,
∴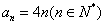 ,
,
又当x≥n时,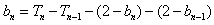 ,∴
,∴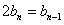 ,
,
∴数列{bn}是等比数列,其首项为1,公比为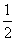 ,
,
∴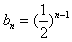 ;
;
(2)由(1)知 ,
,
∴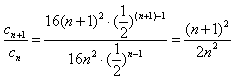 ,
,
由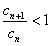 得
得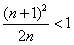 ,即
,即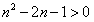 ,
,
∴ ,即n≥3,
,即n≥3,
又n≥3时, 成立,即
成立,即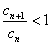 ,
,
由于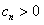 恒成立,
恒成立,
因此,当且仅当n≥3时,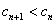 。
。
