问题
填空题
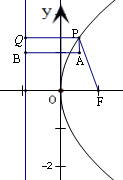
已知抛物线y2=4x的焦点是F,定点A(
|
答案
由题意,抛物线y2=4x的准线为x=-1,焦点是F(1,0).
设P、A在抛物线的准线上的射影分别为Q、B,连结PQ、AB.
根据抛物线的定义,可得|PF|=|PQ|,
∵|PA|+|PF|=|PA|+|PQ|,
∴当|PA|+|PQ|取得最小值时,|PA|+|PF|有最小值.
由平面几何知识,可得当P、Q、A三点共线时,即点P、Q在线段AB上时,
|PA|+|PQ|最小,最小值为
-(-1)=1 2
.3 2
因此,|PA|+|PF|的最小值是
.3 2
故答案为:3 2