问题
解答题
在平面直角坐标系xOy中，直线l：x=-2交x轴于点A，设P是l上一点，M是线段OP的垂直平分线上一点，且满足∠MPO=∠AOP。
（1）当点P在l上运动时，求点M的轨迹E的方程；
（2）已知T（1，-1），设H是E上动点，求|HO|+|HT|的最小值，并给出此时点H的坐标；
（3）过点T（1，-1）且不平行于y轴的直线l1与轨迹E有且只有两个不同的交点，求直线l1的斜率k的取值范围。
答案
解：（1）如图，设MQ为线段OP的垂直平分线，交OP于点Q，
∵
∴
∴
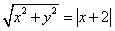，即
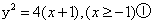
另一种情况（如图2），即点M和A位于OP的同侧
因为MQ为线段OP的垂直平分线
∴
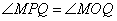
又∵
∴
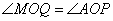
因此M在x轴上，此时，记M（x，0），设P（-2，a）为l上任意点（a∈R）
由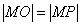
即
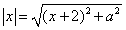得
∴点M（x，0）的轨迹方程为y=0，x≤-1②
综合①②得，点M的轨迹E的方程为
；
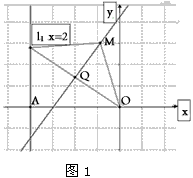
（2）由（1）知，轨迹E的方程由E1和E2两部分组成
当
时，过T做垂直于L的直线，垂足为T′，交E1于点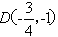
再过H做垂直于L的直线，交l于H
∴
∴
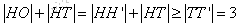（该等号仅当H′与T′重合（或H与D重合）时取得）
当
时，则
综合可得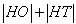
的最小值为3，此时点H
；
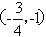（3）由图3可知，直线l1的斜率k不可能为0
设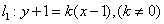
∴
，代入E1的方程得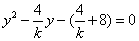
∴
∴l1与E中的E1有且仅有两个不同的交点
又由E2和l1的方程可知，若l1与E2有交点
则此交点的坐标为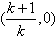
，且
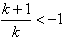，即当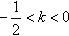
时l1与E2有唯一交点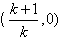
从上可知l1与E有三个不同的交点
∴直线l1斜率k的取值范围是
。