问题
解答题
已知下列数列{an}的前n项和Sn,分别求它们的通项公式an,
(1)Sn=2n2+3n;
(2)Sn=3n+1。
答案
解:(1)当n=1时,a1=S1=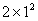 +3×1=5,
+3×1=5,
当n≥2时,an=Sn-Sn-1=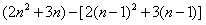 =4n+1,
=4n+1,
当n=1时,4×1+1=5=a1,
∴an=4n+1;
(2)当n=1时,a1=S1=3+1=4,
当n≥2时,an=Sn-Sn-1=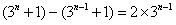 ,
,
当n=1时,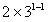 =2≠a1,
=2≠a1,
∴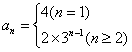 。
。
已知下列数列{an}的前n项和Sn,分别求它们的通项公式an,
(1)Sn=2n2+3n;
(2)Sn=3n+1。
解:(1)当n=1时,a1=S1=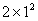 +3×1=5,
+3×1=5,
当n≥2时,an=Sn-Sn-1=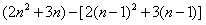 =4n+1,
=4n+1,
当n=1时,4×1+1=5=a1,
∴an=4n+1;
(2)当n=1时,a1=S1=3+1=4,
当n≥2时,an=Sn-Sn-1=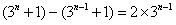 ,
,
当n=1时,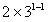 =2≠a1,
=2≠a1,
∴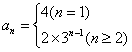 。
。