问题
解答题
已知关于x的方程(k+1)x2+(3k-1)x+2k-2=0.
(1)讨论此方程根的情况;
(2)若方程有两个整数根,求正整数k的值.
答案
(1)当k=-1时,方程-4x-4=0为一元一次方程,此方程有一个实数根;
当k≠-1时,方程(k+1)x2+(3k-1)x+2k-2=0是一元二次方程,
△=(3k-1)2-4(k+1)(2k-2)=(k-3)2.
∵(k-3)2≥0,即△≥0,
∴k为除-1外的任意实数时,此方程总有两个实数根.
综上,无论k取任意实数,方程总有实数根;
(2)∵方程(k+1)x2+(3k-1)x+2k-2=0中a=k+1,b=3k-1,c=2k-2,
∴x=
,1-3k±(k-3) 2(k+1)
∴x1=-1,x2=
-2,4 k+1
∵方程的两个根是整数根,且k为正整数,
∴当k=1时,方程的两根为-1,0;
当k=3时,方程的两根为-1,-1.
∴k=1,3.

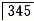 楔状缺损,4探及穿髓孔,叩(++),Ⅰ度松动
楔状缺损,4探及穿髓孔,叩(++),Ⅰ度松动
