问题
解答题
(1)设f(x)=
(2)f(x)为多项式,且
|
答案
(1)
f(x)=lim x→0+
(2x+b)=b,lim x→0+
f(x)=lim x→0-
(1+2x)=2,lim x→0-
当且仅当b=2时,
f(x)=lim x→0+
f(x),故b=2时,原极限存在.lim x→0-
(2)由于f(x)是多项式,且lim x→∞
=1,f(x)-4x3 x
∴可设f(x)=4x3+x2+ax+b(a、b为待定系数).
又∵lim x→0
=5,即f(x) x
(4x2+x+a+lim x→0
)=5,b x
∴a=5,b=0,即f(x)=4x3+x2+5x.

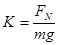 称为载荷值。
称为载荷值。