问题
解答题
动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4,
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)过点Q(0,-1)作曲线C的切线,求所作的切线与曲线C所围成区域的面积.
答案
解:(Ⅰ)设P(x,y),
根据题意,得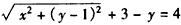 ,
,
化简,得 。
。
(Ⅱ)设过Q的直线方程为y=kx-1,
代入抛物线方程,整理得x2-4kx+4=0,
由△=16k2-16=0,解得k=±1,
于是所求切线方程为y=±x-1,(亦可用导数求得切线方程)
切点的坐标为(2,1),(-2,1),
由对称性知所求的区域的面积为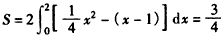 。
。
