问题
解答题
已知：等差数列{an}的公差和等比数列{bn}的公比都是d，（d≠1）且a1=b1，a4=b4，a10=b10；
（1）求数列{an}，{bn}的通项公式；
（2）设数列{bn}的前n和为Tn，求Tn；
（3）b16是否为数列{an}中的项？如果是，是第几项？如果不是，请说明理由．
答案
解：（1）a4=a1+3d，b4=b1d3，
∴a1+3d=a1d3，
∴a1=
，
∵a10=a1+9d，b10=a1d9，
∴a1+9d=a1d9，a1=
，
∴
=
，
∴d9﹣1=3d3﹣3，
∴（d3﹣1）（d6+d3+1）﹣3（d3﹣1）=0，
∵d≠1，∴d6+d3﹣2=0，
∴d3=﹣2．
∴d=﹣
，a1=
=
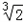，an=a1+（n﹣1）d=（2﹣n）
，bn=
（﹣
） n﹣1；
（2）∵b1=a1=
，d=﹣
，则数列{bn}的前n和为
Tn=
=
（1﹣
）=
﹣
；
（3）b16是{an}中的项，为第34项，理由为：假设b16是{an}中的项，
∵b16=a1d15=
（﹣
）15=﹣32
，an=（2﹣n）
，
∴（2﹣n）
=﹣32
，
解得：n=34，
∴b16是{an}中的项，为第34项．