问题
解答题
在平面直角坐标系xOy中，抛物线C的顶点在原点，焦点F的坐标为(1，0)．
(Ⅰ)求抛物线C的标准方程；
(Ⅱ)设M，N是抛物线C的准线上的两个动点，且它们的纵坐标之积为-4，直线MO，NO与抛物线的交点分别为点A，B，求证：动直线AB恒过一个定点。
答案
解：(Ⅰ)设抛物线的标准方程为y2=2px(p＞0)，则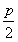
=1，p=2，
所以抛物线C的标准方程为y2=4x。
(Ⅱ)抛物线C的准线方程为x=-1，
设M(-1，y1)，N(-1，y2)，其中y1y2=-4，
则直线MO的方程为：y=-y1x，
将y=-y1x与y2=4x联立方程组，
解得A点坐标为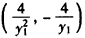
，同理可得B点坐标为
，
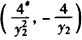则直线AB的方程为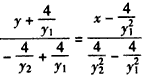
，
整理，得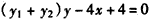
，
由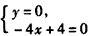
，解得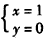
，
故动直线AB恒过一个定点(1，0)。
