问题
解答题
已知抛物线C：y2=mx（m≠0）的准线与直线l：kx-y+2k=0（k≠0）的交点M在x轴上，与C交于不同的两点A、B，线段AB的垂直平分线交x轴于点N（p，0）。
（1）求抛物线C的方程；
（2）求实数p的取值范围；
（3）若C的焦点和准线为椭圆Q的一个焦点和一条准线，试求Q的短轴的端点的轨迹方程。
答案
解：（1）因为点M在x轴上，令y=0代入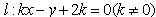
，解得x=-2，
所以M（-2，0），
所以抛物线C：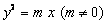
的准线为x=-2=
，
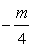所以m=8
所以抛物线C的方程为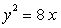
。
（2）由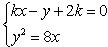
消去x得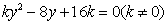
，
∴
∴
，
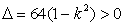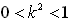
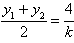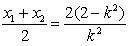
∴AB的中垂线方程为
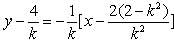
令y=0得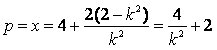
∵
∴
。
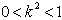
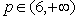（3）∵抛物线焦点F（2，0），准线x=-2
∴x=-2是Q的左准线
设Q的中心为O′（x，0），则短轴端点为（x，±y）
①若F为左焦点，则c=x-2＞0，b=|y|
∴a2=b2+c2=（x-2）2+y2
依左准线方程有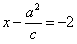
，
∴
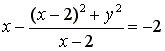
即y2=4（x-2） （x＞2） ；
②若F为右焦点，则0＜x＜2，故c=2-x，b=|y|
∴a2=b2+c2=（2-x）2+y2
依左准线方程有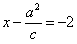
即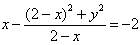
化简得2x2-4x+y2=0
即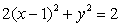
（0＜x＜2，y≠0）。