问题
问答题
设函数f(x)=x-lnx，求f(x)的单调增区间．
答案
参考答案：
函数f(x)的定义域为(0，+∞)．
令y=f(x)，则．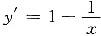
令y’=0，解得x=1．
当0＜x＜1时，y’＜0；当x＞1时，y’＞0．
因此函数f(x)的单调增区间为(1，+∞)．
搜题请搜索小程序“爱下问搜题”
设函数f(x)=x-lnx，求f(x)的单调增区间．
参考答案：
函数f(x)的定义域为(0，+∞)．
令y=f(x)，则．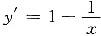
令y’=0，解得x=1．
当0＜x＜1时，y’＜0；当x＞1时，y’＞0．
因此函数f(x)的单调增区间为(1，+∞)．