问题
解答题
根据下列条件求抛物线的标准方程．
(1) 抛物线的焦点是双曲线16x2-9y2=144 的左顶点；
(2) 抛物线焦点在x 轴上，直线y=-3 与抛物线交于点A ，|AF|=5 ．
答案
解：(1)双曲线方程化为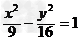
，左顶点为(-3，0)，
由题意设抛物线方程为y2=-2px(p>0)且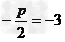
∴p =6
∴抛物线的标准方程为y2=-12x．
(2)设抛物线的标准方程为y2=2px(p≠0)，A（m，-3）．
由抛物线定义得5=|AF|=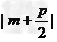
又（-3）2=2pm，
∴p=±1或p=±9，
故所求抛物线的标准方程为y2=±2x或y2=±18x.