参考答案：

(1)记人均收入为y，人均资本为k，由Y=K^αL^1-α，得到人均生产函数：y=Y/L=(K/L)^α=f(k)=k^α。

新古典增长模型假设：经济体的储蓄率s外生，社会储蓄为S=sY；经济体中劳动人口增长率为外生，按不变的比率n增长；生产函数规模报酬不变：Y=F(K，N)，tY=F(tK，tN)，t＞0；边际报酬递减：F′＞O，F″＜O；技术变量外生。

经济均衡时，有I=S。

ΔK=I-8K

S=sY

ΔK=sY-8K

两边同除劳动数量N，得：

ΔK/N=sy-δk，y为人均产出，k为人均资本。

k=K/N，则Δk/k=ΔK/K-ΔN/N=ΔK/K-n

ΔK=(Δk/k)×K+nK

同除N，得ΔK/N=Δk+nk=sy-δk

Δk=sy-(n+δ)k

这是新古典增长模型的基本方程。

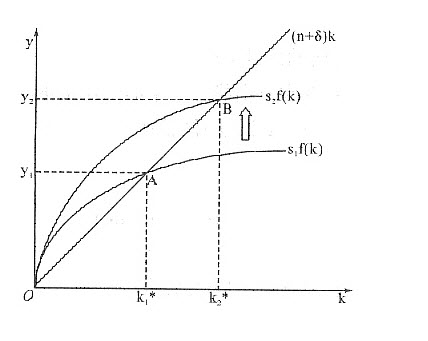
要实现稳态，Δk=sy-(n+δ)k=0，

sy=(n+δ)k，(n+δ)k曲线和sf(k)曲线的交点是稳态点。

由Y=K^αL^1-α，我们可以得到人均生产函数为：y=Y/L=

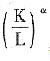=k^α，由稳态条件sy=(n+δ)k有sk^α=(n+δ)k，解得人均资本存量