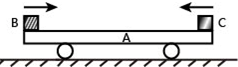
如图所示,光滑水平面上静止放置着一辆平板车A.车上有两个小滑块B和C(都可视为质点),B与车板之间的动摩擦因数为μ,而C与车板之间的动摩擦因数为2μ,开始时B、C分别从车板的左、右两端同时以大小相同的初速度v0相向滑行.经过一段时间,C、A的速度达到相等,此时C和B恰好发生碰撞.已知C和B发生碰撞时两者的速度立刻互换,A、B、C三者的质量都相等,重力加速度为g.设最大静摩擦力大小等于滑动摩擦力.
(1)求开始运动到C、A的速度达到相等时的时间;
(2)求平板车平板总长度;
(3)已知滑块C最后没有脱离平板,求滑块C最后与车达到相对静止时处于平板上的位置.
(1)设A、B、C三个物体的质量都为m,从开始到C、A的速度达到相等的过程所用时间为t,C、A相等的速度为vC,根据动量定理得
对C:-2μmgt=mvC-mv0
对A:(2μmg-μmg)t=mvC
联立解得,t=
,vC=v0 3μg
v01 3
(2)对B,由动量定理得,
-μmgt=mvB-mv0
得到,vB=
v02 3
对C:xC=
t,v0+vC 2
对B:xB=
tv0+vB 2
平板车平板总长度L=xB+xC
解得,L=v 20 2μg
(3)对A:xA=
=xAt 2
,A、B、C三者的位移和末速度分别为:xA=v 20 18μg
,方向向左;v 20 18μg
xB=
,方向向右;xC=5 v 20 18μg
,方向向左.2 v 20 9μg
vA=vC=
v0,方向向左;vB=1 3
v0,方向向右.C和B发生碰撞时两者的速度立刻互换,则碰撞后C和B的速度各为:vC′=2 3
v0,方向向右,vB′=2 3
v0,方向向左.1 3
碰撞后B和A的速度相等,设B和A保持相对静止一起运动,此时对B和A整体有fC=2μmg=2ma
对B:B受到的摩擦力为fB′=ma=μmg,说明B和A保持相对静止一起运动.
设C最后停在车板上时,共同速度为v,由动量守恒定律得
mvC′-2mvB′=2mv
可得,v=0
对这一过程,对C,由动能定理得
-2μmgSC′=0-
m1 2 v ′2C
对B和A整体,由动能定理得
-2μmgSA′=0-
2m1 2 v ′2B
解得,C和A的位移分别是
SC′=
,向右,SA′=2 v 20 9μg
,向左.v 20 18μg
则C先相对于车板向左移动x1=xC-xA=
,后相对于车板向右移动S=SC′-SA′=v 20 6μg
,恰好回到原来的位置,即滑块C最后停在车板的右端.v 20 6μg
答:
(1)开始运动到C、A的速度达到相等时的时间为t=
;v0 3μg
(2)平板车平板总长度L=
;v 20 2μg
(3)滑块C最后停在车板的右端.
