问题
解答题
已知曲线C上的动点P(x,y)满足到点F(0,1)的距离比到直线y=-2的距离小1.
(1)求曲线C的方程;
(2)过点F作直线l与曲线C交于A、B两点.
(ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明:MA⊥MB;
(ⅱ)是否在y轴上存在定点Q,使得无论AB怎样运动,都有∠AQF=∠BQF?证明你的结论.
答案
(1)依题意有
=|y+2|-1,由显然y>-2,得(y-1)2+x2
=|y+1|,化简得x2=4y;(y-1)2+x2
(2)(ⅰ)∵直线AB与x轴不垂直,设AB:y=kx+8.
A(x1,y1),B(x2,y2).
由
可得x2-4kx-4=0,x1+x2=4k,x1x2=-4y=kx+1 y=
x2.1 4
抛物线方程为y=
x2,求导得y′=1 4
x.1 2
所以过抛物线上A、B两点的切线斜率分别是kAM=
x1,kBM=1 2
x2,1 2
∴kAM•kBM=
x1×1 2
x2=1 2
x1x2=-1即AM⊥BM1 4
(ⅱ)设点Q(0,t),此时kAQ=
,kBQ=y1-t x1
,y2-t x2
由(ⅰ)可知故kAQ+kBQ=
+
-tx12 4 x1
=
-tx22 4 x2
=0对一切k恒成立x1x2(x1+x2)-4t(x1+x2) 4x1x2
即:k(8+t)=0
故当t=-1,即Q(0,-1)时,使得无论AB怎样运动,都有∠AQP=∠BQP

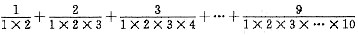 的值为( ).
的值为( ). 