问题
问答题
求幂级数
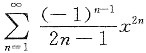的收敛域及和函数．
答案
参考答案：
[分析]： 用比值判别法确定收敛区间，进而确定收敛域；利用幂级数的逐项求导求和函数．
[详解] 因为
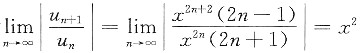，所以当x2＜1，即-1＜x＜1时，原幂级数绝对收敛．
当x=±1时，级数为
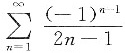，由莱布尼兹判别法显然收敛，故原幂级数的收敛域为[-1，1]．
又
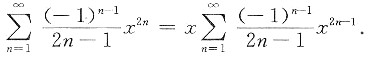
令
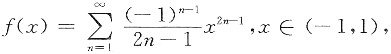
则
由于f(0)=0，所以
从而幂级数的收敛域为[-1，1]，和函数为xarctanx，x∈[-1，1]．
