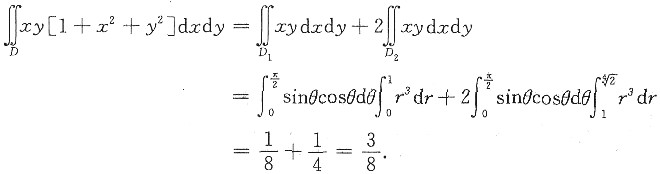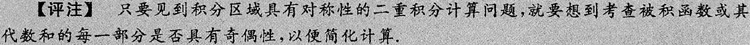问题
问答题
设D=(x，y)|x2+y2≤
，x≥0，y≥0，[1+x2+y2]表示不超过1+x2+y2的最大整数．计算二重积分
．
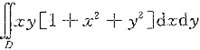答案
参考答案：
[分析]： 首先应设法去掉取整函数符号，为此将积分区域分为两部分即可．
[详解] 令D1={(x，y)|0≤x2+y2＜1，x≥0，y≥0}，
则
搜题请搜索小程序“爱下问搜题”
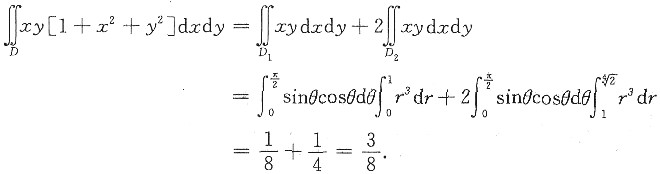
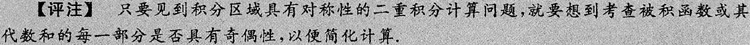
设D=(x，y)|x2+y2≤
，x≥0，y≥0，[1+x2+y2]表示不超过1+x2+y2的最大整数．计算二重积分
．
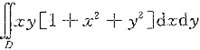参考答案：
[分析]： 首先应设法去掉取整函数符号，为此将积分区域分为两部分即可．
[详解] 令D1={(x，y)|0≤x2+y2＜1，x≥0，y≥0}，
则