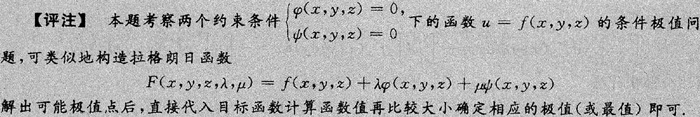问题
问答题
求函数u=x2+y2+z2在约束条件z=z2+y2和x+y+z=4下的最大和最小值。
答案
参考答案：[详解] 设拉格朗日函数为
F(x，y，z)=x2+y2+z2+λ(z-x2-y2)+μ(x+y+z-4)，
解方程组
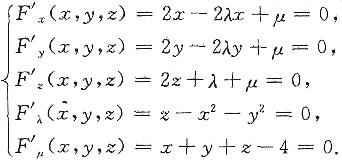
得
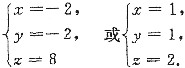
故最大值、最小值分别为μmax=(-2)2+(-2)2+82=72，μmin=12+12+22=6．
搜题请搜索小程序“爱下问搜题”
求函数u=x2+y2+z2在约束条件z=z2+y2和x+y+z=4下的最大和最小值。
参考答案：[详解] 设拉格朗日函数为
F(x，y，z)=x2+y2+z2+λ(z-x2-y2)+μ(x+y+z-4)，
解方程组
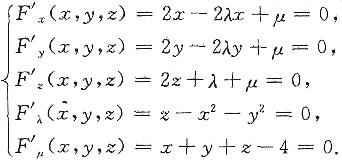
得
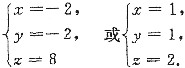
故最大值、最小值分别为μmax=(-2)2+(-2)2+82=72，μmin=12+12+22=6．