问题
问答题
设y=y(x)是区间(-π，π)内过
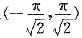的光滑曲线，当-π＜x＜0时，曲线上任一点处的法线都过原点；当0≤x＜π时，函数满足y"+y+x=0．求y(x)的表达式．
答案
参考答案：[详解] 由题意知，当-π＜x＜0时，
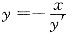，即ydy=-xdx，可得
y2=-x2+C．
由初始条件
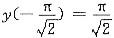，得C=π2，所以
．
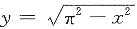当0≤x＜π时，y*+y+x=0，
y"+y=0的通解为y"=C1cosx+C2sinx，
令y"+y+x=0的特解为y1=ax+b，
则有0+ax+b+x=0，得a=-1，b=0，故y1=-x，
因而y"+y+x=0的通解为y=C1cosx+C2sinx-x，
由于y=y(x)是(-π，π)内的光滑曲线，故y在x=0处连续，
于是由y(0-)=π，y(0+)=C1，故C1=π时，y=y(x)在x=0处连续．
又当-π＜x＜0时，有2x+2yy’=0得
；
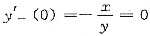当0≤x＜π时，有y’=-C1sinx+C2cosx-1得y’+(0)=C2-1．
由y’+(0)=y’-(0)，C2-1=0，即C2=1
故y=y(x)的表达式为
．
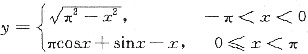