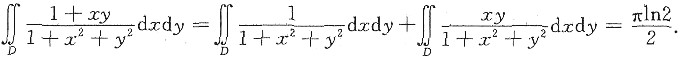问题
问答题
设区域D=(x,y)|x2+y2≤1,x≥0,计算二重积分
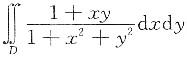 .
.
答案
参考答案:
[分析]: 由于积分区域D关于x轴对称,故可先利用二重积分的对称性结论简化所求积分,又积分区域为圆域的一部分,则将其化为极坐标系下累次积分即可.
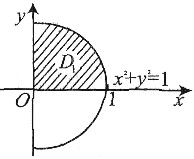
[详解] 积分区域D如右图所示.因为区域D关于x轴对称,函数
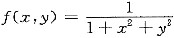 是变量y的偶函数,
是变量y的偶函数,
函数
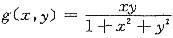 是变量y的奇函数.则
是变量y的奇函数.则
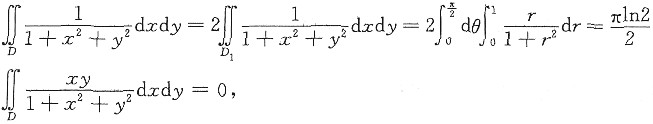
故
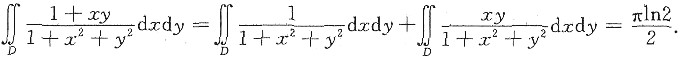

设区域D=(x,y)|x2+y2≤1,x≥0,计算二重积分
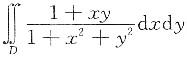 .
.
参考答案:
[分析]: 由于积分区域D关于x轴对称,故可先利用二重积分的对称性结论简化所求积分,又积分区域为圆域的一部分,则将其化为极坐标系下累次积分即可.
[详解] 积分区域D如右图所示.因为区域D关于x轴对称,函数
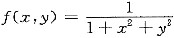 是变量y的偶函数,
是变量y的偶函数,
函数
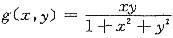 是变量y的奇函数.则
是变量y的奇函数.则
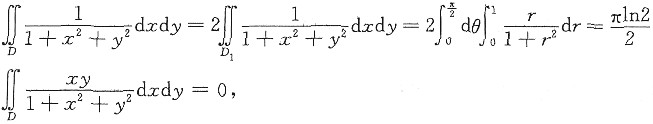
故