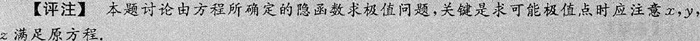问题
问答题
设z=z(x，y)是由x2-6xy+10y2-2yz-z2+18=0确定的函数，求z=z(x，y)的极值点和极值．
答案
参考答案：
[分析]： 可能极值点是两个一阶偏导数为零的点，先求出一阶偏导，再令其为零确定极值点即可，然后用二阶偏导确定是极大值还是极小值，并求出相应的极值．
[详解] 因为x2-6xy+10y2-2yz-z2+18=0，所以
令
故
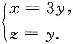将上式代入x2-6xy+10y2-2yz-z2+18=0，可得
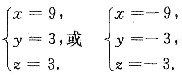
由于
所以
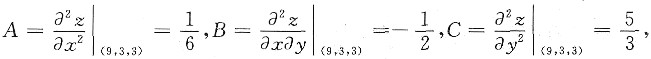
故
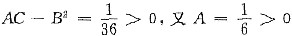，从而点(9，3)是z(x，y)的极小值点，极小值为z(9，3)=3．
类似地，由
可知
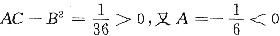，从而点(-9，-3)是z(x，y)的极大值点，极大值为z(-9，-3)=-3
