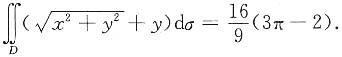问题
问答题
求
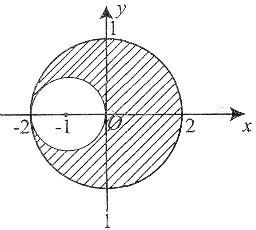
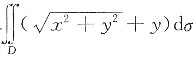 ,其中D是由圆x2+y2=4和(x+1)2+y2=1所围成的平面区域(如图).
,其中D是由圆x2+y2=4和(x+1)2+y2=1所围成的平面区域(如图).
答案
参考答案:
[分析]: 首先,将积分区域D分为大圆D1={(x,y)|x2+y2≤4)减去小圆D2={(x,y)|(x+1)2+y2≤1),再利用对称性与极坐标计算即可.
[详解] 令D1={(x,y)|x2+y2≤4),D2={(x,y)|(x+1)2+y2≤1),
由对称性,
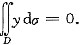
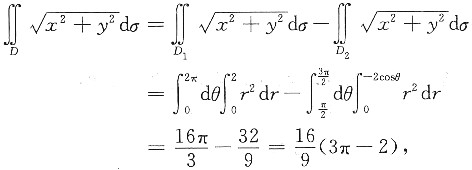
所以
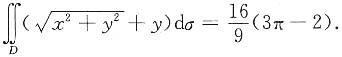

求
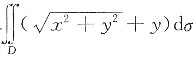 ,其中D是由圆x2+y2=4和(x+1)2+y2=1所围成的平面区域(如图).
,其中D是由圆x2+y2=4和(x+1)2+y2=1所围成的平面区域(如图).

参考答案:
[分析]: 首先,将积分区域D分为大圆D1={(x,y)|x2+y2≤4)减去小圆D2={(x,y)|(x+1)2+y2≤1),再利用对称性与极坐标计算即可.
[详解] 令D1={(x,y)|x2+y2≤4),D2={(x,y)|(x+1)2+y2≤1),
由对称性,
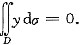
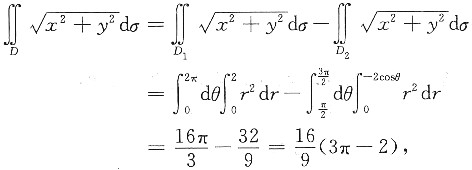
所以