问题
单项选择题
已知函数f(x，y)在点(0，0)的某个邻域内连续，且
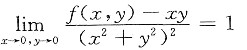，则
(A) 点(0，0)不是f(x，y)的极值点．
(B) 点(0，0)是f(x，y)的极大值点．
(C) 点(0，0)是f(x，y)的极小值点．
(D) 根据所给条件无法判断点(0，0)是否为f(x，y)的极值点．
答案
参考答案：A
解析： 由
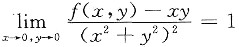知，分子的极限必为零，从而有f(0，0)=0，且
f(x，y)-xy≈(x2+y2)2(|x|，|y|充分小时)，于是
f(x，y)-f(0，0)≈xy+(x2+y2)2．
可见当y=x且|x|充分小时，f(x，y)-f(0，0)≈x2+4x4＞0；而当y=-x且|x|充分小时，f(x，y)-f(0，0)≈-x2+4x4＜0．故点(0，0)不是f(x，y)的极值点，应选(A)．
