Casablanca, Sep. 24
A flash flood swept across the coastal plain about 100 miles southwest of here, killing hundreds of Moroccans in a market place yesterday morning.
Reports from the area said 218 bodies had been counted, and many of the people were missing.
The flood followed heavy rains, which filled the coastal plain and dried river beds and caused them to overflow. The flood crest, sev eral feet high, hit the village of Khemis Nagua at midmorning yesterday as farmers from the surrounding area joined town people in an o
eral feet high, hit the village of Khemis Nagua at midmorning yesterday as farmers from the surrounding area joined town people in an o pen market place.
pen market place.
The roaring water swept the village’s living places, the market sheds (棚子), shoppers, cattle and farm tools for miles across the plain..
The flood was over almost as soon as it started, the reports said, as the cre st swept out to sea. Rescue workers quickly moved into the area from Sari, about 25 miles further south.
st swept out to sea. Rescue workers quickly moved into the area from Sari, about 25 miles further south.
小题1: It can be learnt from the te xt that _____.
xt that _____.
A.the news report is from Khemis Nagua
B.the flo od didn’t last long
od didn’t last long
C.hundreds of Moroccans were saved
D.Casablanca is a city in Africa小题2: The report mainly tells the public about _____.
A.how the flood swept the coastal plain
B.why the terrible flood took place
C.the flash flood in the fall
D.a rescue attempt小题3:According to the text, which of the following maps may be correct?
(KN="Khemis" Nagua C="Casablanca " S=Safi)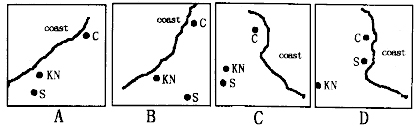

 eral feet high, hit the village of Khemis Nagua at midmorning yesterday as farmers from the surrounding area joined town people in an o
eral feet high, hit the village of Khemis Nagua at midmorning yesterday as farmers from the surrounding area joined town people in an o pen market place.
pen market place. st swept out to sea. Rescue workers quickly moved into the area from Sari, about 25 miles further south.
st swept out to sea. Rescue workers quickly moved into the area from Sari, about 25 miles further south. xt that _____.
xt that _____. od didn’t last long
od didn’t last long