问题
问答题
k为何值时，线性方程组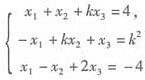
，有唯一解、无解、有无穷多组解在有解的情况下，求出其全部解。
答案
参考答案：
用初等行变换化增广矩阵为阶梯形
当k≠-1和k≠4时，有
。
这时方程组有唯一解：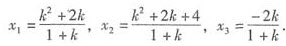
当k=-1时，r(A)=2＜r(A)=3，方程组无解．
当k=4时，有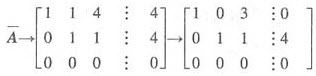
，r(A)=r(A)=2＜n=3，
故方程组无穷多组解，这时，同解方程组为：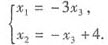
令x3=c，得方程组的全部解：
，其中c为任意常数．
解析：
[考点] 这是对带一个未知参数的非齐次方程组解的讨论，可用初等行变换法