问题
单项选择题
设y=f(x)是满足微分方程y"+y’-esinx=0的解,且f’(x0)=0,则f(x)在()。
A.x0的某个邻域内单调增加
B.x0的某个邻域内单调减少
C.x0处取得极小值
D.x0处取得极大值
答案
参考答案:C
解析:
[考点] 将f’(x0)=0代入方程,得f"(x0)的符号,从而由极值的充分条件得选项
f(x)满足方程f"(x)+f’(x)-esinx=0,
所以有f"(x0)=esinx-f’(x0)=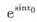 >0,
>0,
即f’(x0)=0,f"(x0)>0,故f(x)在x0处取得极小值.故选(C).
