问题
问答题
设f(x)在闭区间[0,c]上连续,其导数f’(x)在开区间(0,c)内存在且单调减少,f(0)=0.试应用拉格朗日中值定理证明不等式:f(a+b)≤f(a)+f(b),其中常数a,b满足条件0≤a≤b≤a+b≤C。
答案
参考答案:
当a=0时,f(0)=0,有f(a+b)=f(b)=f(a)+f(b);
当a>0时,在[0,a]和[b,a+b]上分别应用拉格朗日中值定理有
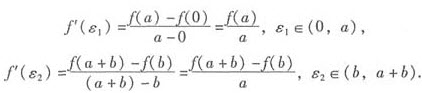
显然0<ε1<a≤b<ε2<a+b≤c,因f’(x)在[0,c]上单调减少,
故f’(ε2)≤f’(ε1),从而有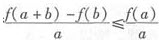 ,
,
因为a>0,所以有f(a+b)≤f(a)+f(b).
总之,当0≤a≤b≤a+b≤c时,f(a+b)≤f(a)+f(b)总成立.
解析:
[考点] 在[0,a]与[b,a+b]上分别应用拉格朗日中值定理
