问题
单项选择题
设n阶矩阵A非奇异(n≥2),A*是矩阵A的伴随矩阵,则()。
A.(A*)*=|A|n-1A
B.(A*)*=|A|n+1A
C.(A*)*=|A|n-2A
D.(A*)*=|A|n+2A
答案
参考答案:C
解析:
[考点] 利用伴随矩阵的性质和行列式的性质即可
涉及伴随矩阵A*,首先联想到公式AA*=A*A=|A|E.
由题设,矩阵A非奇异,故A可逆,所以由公式AA*=A*A=|A|E可得A*=|A|A-1,
于是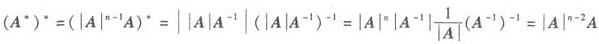 ,
,
故应选(C).
