问题
解答题
已知直线l1:y=4x和P(6,4)在直线l1上求一点Q,使过PQ的直线与l1,以及x轴,在第Ⅰ象限内围成的三角形的面积最小。
答案
解:设Q点坐标为(x1,y1),y1= 4x1,则直线的方程为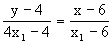

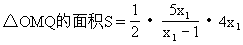
 (1)
(1)
要使方程(1)有实根,则S2-40S≥0,即 S≥40
把S=40代入(1),解得x1=2,这就是说,当x1=2时,S达到最小。故所求点Q的坐标为(2,8)
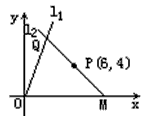
已知直线l1:y=4x和P(6,4)在直线l1上求一点Q,使过PQ的直线与l1,以及x轴,在第Ⅰ象限内围成的三角形的面积最小。
解:设Q点坐标为(x1,y1),y1= 4x1,则直线的方程为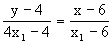

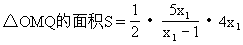
 (1)
(1)
要使方程(1)有实根,则S2-40S≥0,即 S≥40
把S=40代入(1),解得x1=2,这就是说,当x1=2时,S达到最小。故所求点Q的坐标为(2,8)
