问题
问答题
是否存在常数n,使得存在可微函数u(x,y)在如下区域D满足:
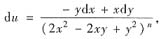
若存在,并求出相应的u(x,y).
(Ⅰ) D:x2+y2>0;(Ⅱ)D:x≠0.
答案
参考答案:[分析与求解] 若存在常数n与u(x,y)满足题中要求,则必有

上式成立的充要条件是n=1.
因此,n≠1时,
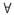 区域D,均不存在这种u(x,y);n=1时,还需考察区域D的单连通性.
区域D,均不存在这种u(x,y);n=1时,还需考察区域D的单连通性.
(Ⅰ)D:x2+y2>0,不是单连通区域,上述必要条件导出n=1不足以保证存在原函数.取环绕原点的闭曲线C:2x2-2xy+y2=1,并取逆时针方向,则
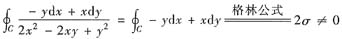
其中σ是C所围区域的面积.
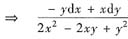 在D不存在原函数.
在D不存在原函数.
因此,不存在常数n,在区域D:x2+y2>0上满足题中的要求.
(Ⅱ)D:x≠0,即x>0或x<0.这是单连通区域,在D上存在可微函数u(x,y)满足题中要求的充要条件是n=1.由于
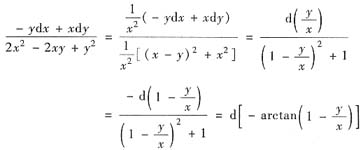
因此
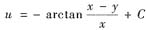 ,其中C为
,其中C为
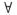 常数.
常数.

