问题
问答题
设随机变量X的概率密度函数为
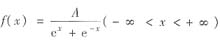 ,对X进行两次独立观察,
,对X进行两次独立观察,
其结果分别记为X1,X2,令
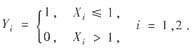
(Ⅰ) 确定常数A,并计算概率PX1<0,X2<1;
(Ⅱ) 求二维随机变量(Y1,Y2)的联合概率分布;
(Ⅲ) 求二维随机变量(Y1,Y2)的联合分布函数.
答案
参考答案:[解] (Ⅰ)由
 ,即
,即

显然,X1与X2独立且与X同分布,因而有

(Ⅱ)由于Y1,Y2均为离散型随机变量,且都可取值1,0,则由题设可得其联合概率分布


于是(Y1,Y2)的联合概率分布见右表,其中


(Ⅲ)如右图,

当(y1,y2)∈D0,即y1<0或y2<0时,F(y1,y2)=0;
当(y1,y2)∈D,即0≤y1<1,0≤y2<1时,
F(y1,y2)=P{Y1≤y1,Y2≤y2}
=P{Y1=0,Y2=0}=P11;
当(y1,y2)∈D1,即0≤y1<1,y2≥1时,
F(y1,y2)=P{Y1≤y1,Y2≤y2}
=P{Y1=0,Y2=0}+P{Y1=0,Y2=1}
P11+P12;
当(y1,y2)∈D2,即y1≥1,0≤y2<1时,
F(y1,y2)=P{Y1=0,Y2=0}+P{Y1=1,Y2=0}=P11+P21;
当(y1,y2)∈D3,即y1≥1,y2≥1时,
F(y1,y2)=P{Y1≤y1,Y2≤y2}
=P{Y1≤1,Y2≤1}=1.
于是(Y1,Y2)的联合分布函数为


