问题
解答题
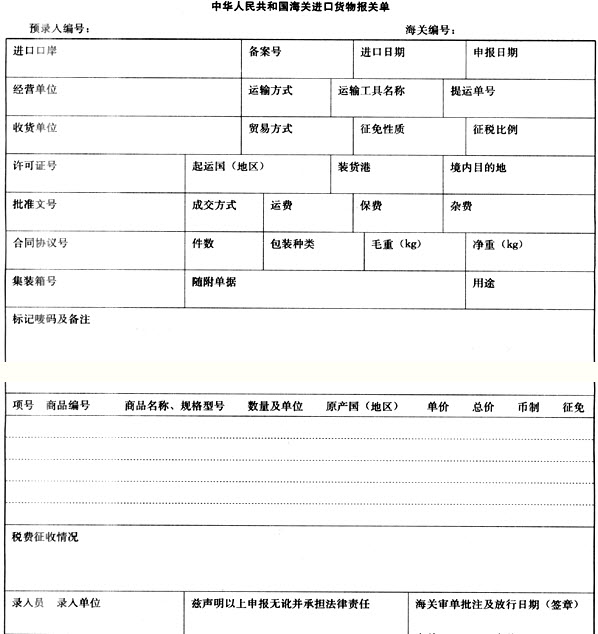
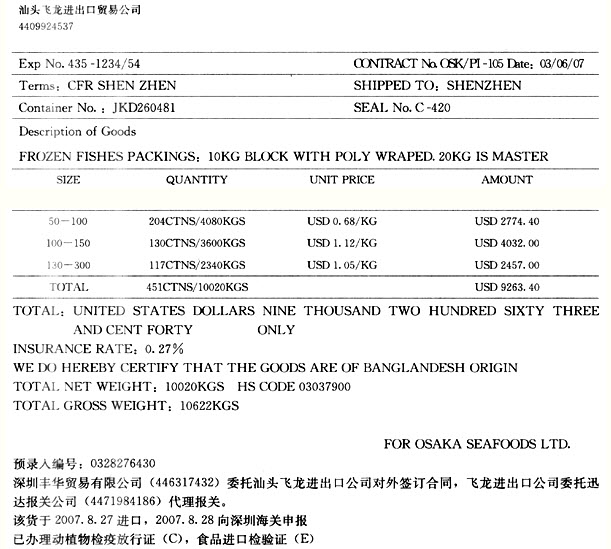
已知焦点在x轴上的抛物线C经过点(3,6).
(1)求抛物线C的标准方程;
(2)直线l:y=kx-3过抛物线C的焦点且与抛物线C交于A、B两点,求A、B两点距离.
答案
(1)设抛物线方程为y2=ax
∵抛物线C经过点(3,6),
∴36=3a,∴a=12
∴抛物线C的标准方程为y2=12x;
(2)将焦点(3,0)代入y=kx-3得直线l方程为y=x-3,
由
消去x可得y2-12y+36=0,∴y=6±6y=x-3 y2=12x 2
∴x=9±62
∴|AB|=
=24.288+288