问题
问答题
设xOy平面第一象限中有曲线F:y=y(x),过点A(0,
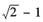 ),y’(x)>0.又M(x,y)为
),y’(x)>0.又M(x,y)为
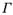 上任意一点,满足:弧段
上任意一点,满足:弧段
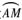 的长度与点M处
的长度与点M处
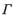 的切线在x轴上的截距之差为
的切线在x轴上的截距之差为
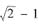 .
.
(Ⅰ) 导出y=y(x)满足的积分、微分方程和初始条件;
(Ⅱ) 求曲线
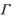 的表达式.
的表达式.
答案
参考答案:[分析与求解] (Ⅰ)先求出,在点M(x,y)处的切线方程
Y-y(x)=y’(x)(X-x),
其中(X,Y)是切线上点的坐标.在切线方程中令Y=0,得x轴上的截距
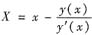
又弧段
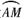 的长度为
的长度为
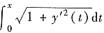 按题意得
按题意得
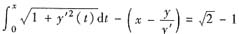 ①
①
这是积分、微分方程,两边对x求导,就可转化为二阶微分方程:
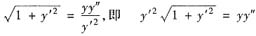
又由条件及①式中令x=0得
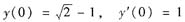
因此得初值问题
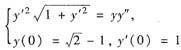
问题①与②是等价的.
(Ⅱ)下面求解②.这是不显含x的二阶方程,作变换p=y’,并以y为自变量得
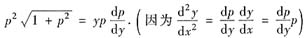
分离变量得
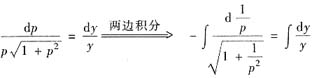 .得
.得
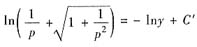
由
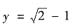 时
时
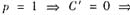

将上面两式相减
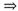

再积分得
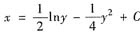
其中
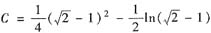 .则③就是所求曲线
.则③就是所求曲线
 的表达式.
的表达式.
