问题
问答题
已知α1=(1，3，5，-1)T，α2=(2，7，α，4)T，α3=(5，17，-1，7)T，
(Ⅰ) 若α1，α2，α3线性相关，求α的值；
(Ⅱ) 当α=3时，求与α1，α2，α3都正交的非零向量α4；
(Ⅲ) 当α=3时，证明α1，α2，α3，α4可表示任一个4维列向量．
答案
参考答案：[解] (Ⅰ)α1，α2，α3线性相关
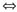秩r(α1，α2，α3)＜3．由于
所以α=-3．
(Ⅱ)设α4=(x1，x2，x3，x4)T，则有(α1，α4)=0，(α2，α4)=0，(α3，α4)=0，即
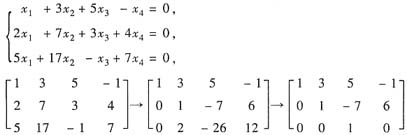
所以α4=k(19，-6，0，1)T，其中k≠0．
(Ⅲ)由于
所以x1α1+x2α2+x3α3+x4α4=α恒有解，即任-4维列向量必可由α1，α2，α3，α4线性表出．
或者由(Ⅰ)知α=3时，α1，α2，α3必线性无关，那么：若
k1α1+k2α2+k3α3+k4α4=0，
用
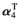左乘上式两端并利用
，有
，又α4≠0，故必有k4=0．于是k1α1+k2α2+k3α3=0．由α1，α2，α3线性无关知必有k1=0，k2=0，k3=0，从而α1，α2，α3，α4必线性无关．而5个4维列向量必线性相关，因此任一个4维列向量都可由α1，α2，α3，α4线性表出．