已知:关于x的方程:mx2-(3m-1)x+2m-2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(1)①当m=0时,原方程可化为x-2=0,解得x=2;
②当m≠0时,方程为一元二次方程,
△=[-(3m-1)]2-4m(2m-2)
=m2+2m+1
=(m+1)2≥0,故方程有两个实数根;
故无论m为何值,方程恒有实数根.
(2)∵二次函数y=mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2,
∴
=2,[-(3m-1)]2-4m(2m-2) |m|
整理得,m2-m=0,
解得m1=0(舍去),m2=1.
则函数解析式为y=x2-2x.

 2NH3。氨气具有可燃性,燃烧时发热量高。近年,科学家发现用催化剂在常温下就能合成氨气,使其有望成为替代氢能的新一代能源。
2NH3。氨气具有可燃性,燃烧时发热量高。近年,科学家发现用催化剂在常温下就能合成氨气,使其有望成为替代氢能的新一代能源。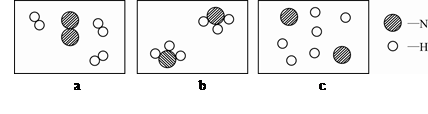
 2X+6H2O,其中X是________。
2X+6H2O,其中X是________。