问题
问答题
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立。根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为0.5,0.6,0.4。经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为ξ,求随机变量ξ的期望。
答案
参考答案:
分别记甲、乙、丙经第一次烧制后合格为事件A1,A2,A3,
(1)设事件E表示第一次烧制后恰好有一件合格,则
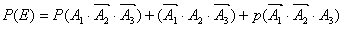

(2)分别记甲、乙、丙经过两次烧制后合格为事件A,B,C,则
P(A)=P(B)=P(C)=0.3,
所以P(ξ=0)=(1-0.3)3=0.343;
P(ξ=1)=3×(1-0.3)2×0.3=0.441;
P(ξ=2)=3×0.32×(1-0.3)=0.189;
P(ξ=3)=0.33=0.027,
故E(ξ)=0×0.343+1×0.441+2×0.189+3×0.027=0.9。

