阅读下列说明和C代码，回答问题。

[说明]

堆数据结构定义如下。

对于n个元素的关键字序列a₁，a₂，…，a_n，当且仅当满足下列关系时称其为堆。

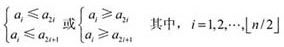
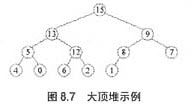
在一个堆中，若堆顶元素为最大元素，则称为大顶堆；若堆顶元素为最小元素，则称为小顶堆。堆常用完全二叉树表示，图8.7是一个大顶堆的例子。

堆数据结构常用于优先队列中，以维护由一组元素构成的集合。对应于两类堆结构，优先队列也有最大优先队列和最小优先队列，其中最大优先队列采用大顶堆，最小优先队列采用小项堆。以下考虑最大优先队列。

假设现已建好大顶堆A，且已经实现了调整堆的函数heapify(A，n，index)。

下面将C代码中需要完善的3个函数说明如下。

(1) heapMaximum(A)：返回大项堆A中的最大元素。

(2) heapExtractMax(A)：去掉并返回大顶堆A的最大元素，将最后一个元素“提前”到堆顶位置，并将剩余元素调整成大顶堆。

(3) maxHeapInsert(A，key):把元素key插入到大顶堆A的最后位置，再将A调整成大顶堆。

优先队列采用顺序存储方式，其存储结构定义如下。

#define PARENT (i) i/2

typedef struct array

int *int_array;//优先队列的存储空间首地址

int array_size;//优先队列的长度

int capacity;//优先队列存储空间的容量

ARRAY;

[C代码]

(1)函数heapMaximum

int heapMaximum(ARRAY *A) return (1) ;

(2)函数heapExtractMax

int_heapExtractMax (ARRAY *A)

int max;

max=A-＞int_array[0]；

(2) ;

A-＞array_size--;

Heapify (A,A-＞array_size,0);//将剩余元素调整成大顶堆

return max;

)

(3)函数maxHeaplnsert

int maxHeaplnsert (ARRAY *A,int key)

int i,*p;

if (A-＞array-size==A-＞capacity)//存储空间的容量不够时扩充空间

p=(int*) realloc (A-＞int array, A-＞capacity *2*sizeof (int));

if(!p) return-1;

A-＞int_array=P;

A-＞capacity=2 *A-＞capacity;

A-＞array_size++:

i= (3) ；

while(i＞0＆＆ (4) )

A-＞int_array [i]=A-＞int_array[PARENT (i)];

i=PARENT (i);

(5) ;

return 0;

[问题1]

根据以上说明和C代码，填充C代码中的空(1)～(5)。

[问题2]

根据以上C代码，函数heapMaximum, heapExtractMax和maxHeaplnsert的时间复杂度的紧致上界分别为 (6) 、 (7) 和 (8) (用O符号表示)。

[问题3]

若将元素10插入到堆A=(15, 13,9，5，12,8，7，4，0，6，2，1)中，调用maxHeaplnsert函数进行操作，则新插入的元素在堆A中第 (9) 个位置(从1开始)。