已知点P是直角坐标平面内的动点，点P到直线x=-p2-1（p是正常数）

问题解答题

已知点P是直角坐标平面内的动点，点P到直线x=-

-1（p是正常数）的距离为d₁，到点F(

，0)的距离为d₂，且d₁-d₂=1．（1）求动点P所在曲线C的方程；
（2）直线l 过点F且与曲线C交于不同两点A、B，分别过A、B点作直线l1：x=-

的垂线，对应的垂足分别为M、N，求证=

•

=0；
（3）记S₁=S_△FAM，S₂=S_△FMN，S₃=S_△FEN（A、B、M、N是（2）中的点），λ=

S1S3

，求λ 的值．

答案

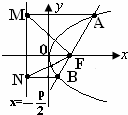
解　（1）设动点为P（x，y），（1分）

依据题意，有|x+

+1|-

(x-

)2+y2

=1，化简得y²=2px．（4分）

因此，动点P所在曲线C的方程是：y²=2px．（6分）

（2）由题意可知，当过点F的直线l（3）的斜率为0时，不合题意，

故可设直线l：x=my-1，如图所示．（8分）

联立方程组

y2=2px

x=my+

，可化为y²-2mpy-p²=0，

则点A（x₁，y₁）、B（x₂，y₂）的坐标满足

y1+y2=2mp

y1y2=-p2

．（10分）

又AM⊥l₁、BN⊥l₁，可得点M(-

，y1)、N(-

，y2)．

于是，

=(-p，y1)，

=(-p，y2)，

因此

•

=(-p，y1)•(-p，y2)=p2+y1y2=0．（12分）

（3）依据（2）可算出x₁+x₂=m（y₁+y₂）+p=2m²p+p，x1x2=

•

，

则S1S3=

(x1+

)|y1|•

(x2+

)|y2|=

•[x1x2+

(x1+x2)+

p4(m2+1)，

|y1-y2|•p)2=

[(y1+y2)2-4y1y2]=p⁴（1+m²）．（16分）

所以，λ=

S1S3

=4即为所求．（18分）