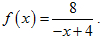问题
问答题
设函数f(x)在定义域I上的导数大于零，若对任意的x0∈I，由线y=f(x)在点（x0，f(x0)）处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式。
答案
参考答案：
设f(x)在点（x0，f(x0)）处的切线方程为：y-f(x0)=f′(x0)(x-x0),
令y=0，得到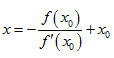
，
故由题意，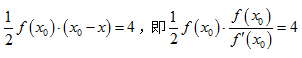
，可以转化为一阶微分方程，
即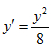
，可分离变量得到通解为：
，
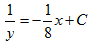已知y(0)=2,得到C=1/2，因此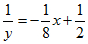
；
即