问题
解答题
已知抛物线W：y=ax2经过点A（2，1），过A作倾斜角互补的两条不同直线l1，l2．
（Ⅰ）求抛物线W的方程及准线方程；
（Ⅱ）当直线l1与抛物线W相切时，求直线l2的方程
（Ⅲ）设直线l1，l2分别交抛物线W于B，C两点（均不与A重合），若以线段BC为直径的圆与抛物线的准线相切，求直线BC的方程．
答案
（Ⅰ）由于A（2，1）在抛物线y=ax2上，所以1=4a，即a=
．1 4
故所求抛物线的方程为y=
x2，其准线方程为y=-1．1 4
（Ⅱ）当直线l1与抛物线相切时，由y'|x=2=1，可知直线l1的斜率为1，其倾斜角为45°，
所以直线l2的倾斜角为135°，故直线l2的斜率为-1，所以l2的方程为y=-x+3
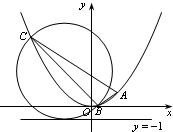（Ⅲ）不妨设直线AB的方程为y-1=k（x-2）（k＞0），
由
得x2-4kx+8k-4=0，y-1=k(x-2) y=
x21 4
易知该方程有一个根为2，所以另一个根为4k-2，
所以点B的坐标为（4k-2，4k2-4k+1），
同理可得C点坐标为（-4k-2，4k2+4k+1）．
所以|BC|=
=[(4k-2)-(-4k-2)]2+[(4k2-4k+1)-(4k2+4k+1)]2
=8(8k)2+(-8k)2
k，．2
线段BC的中点为（-2，4k2+1），因为以BC为直径的圆与准线y=-1相切，
所以4k2+1-(-1)=4
k，由于k＞0，解得k=2
．2 2
此时，点B的坐标为(2
-2，3-22
)，点C的坐标为(-22
-2，3+22
)，2
直线BC的斜率为
=-1，(3+2
)-(3-22
)2 (-2
-2)-(22
-2)2
所以，BC的方程为y-(3-2
)=-[x-(22
-2)]，即x+y-1=0．2