问题
单项选择题
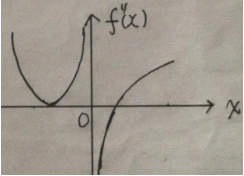
设函数f（x）在（-∞，+∞）内连续，其中二阶导数f″（x）的图形如图所示，则曲线y=f（x）的拐点的个数为（）。
A.0
B.1
C.2
D.3
答案
参考答案：C
解析：
拐点出现在二阶导数等于0，或二阶导数不存在的点，并且在这点的左右两侧二阶导函数异号。因此，由f″（x）的图形可得，曲线y=f（x）存在两个拐点，故选（C）。
搜题请搜索小程序“爱下问搜题”
设函数f（x）在（-∞，+∞）内连续，其中二阶导数f″（x）的图形如图所示，则曲线y=f（x）的拐点的个数为（）。
A.0
B.1
C.2
D.3
参考答案：C
解析：
拐点出现在二阶导数等于0，或二阶导数不存在的点，并且在这点的左右两侧二阶导函数异号。因此，由f″（x）的图形可得，曲线y=f（x）存在两个拐点，故选（C）。