问题
问答题
设函数f(x)在[a,b](a>0)上连续,在(a,b)内可微,且f’(x)≠0.证明存在ξ,η,ζ∈(a,b),使得
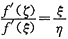
答案
参考答案:[证明] 令g(x)=lnx,则g(x)与f(x)在[a,b]上满足柯西中值定理的条件,故存在ξ∈(a,b),使得
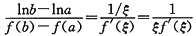 ,即lnb-lna=
,即lnb-lna=
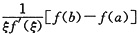 ,
,
从而
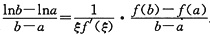 ①
①
分别对g(x),f(x)在[a,b]上使用拉格朗日中值定理,则分别存在η,ζ∈(a,b)使得
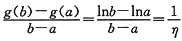 ,②
,②
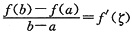 ③
③
将式②与式③代入式①得
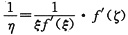 ,即
,即

解析: 由
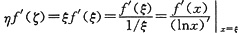 ,
,
应想到先对f(x)与g(x)=lnx使用柯西中值定理,产生一个中值ξ.再对这两个函数的差lnb-lna与f(b)-f(a)凑成可使用拉格朗日中值定理的形式,再分别使用该定理又可得到两个η与ζ.
