参考答案：x(ax²+bx+c)

解析： 先求出对应齐次方程的特征方程的根r₁，r₂，再根据方程右端所含的自由项f(x)的形式设出特解y^*的形式．
(1)若f(x)=P_m(x)e^λx，则特解y^*=x_kQ_m(x)e^λx，其中Q_m(x)是与P_m(x)同次的待定多项式

(2)若f(x)=e^λx[P_t(x)cosoωx+P_n(x)sinωx]，则设特解为
y^*-x^ke^λx[

]，
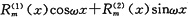其中

，

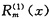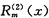是m次多项式，m=max{l，n}，

对应齐次方程的特征方程为
r²+r=r(r+1)=0，
故r=0为其一特征根，而
f(x)=x²=x²e^0x，
即f(x)中的指数为0．因指数0为其特征方程的单根，故特解形式为
y^*=x(ax²+bx+c)，
其中a，b，c为待定的系数．