问题
单项选择题
设f(x)在(a，b)内可微，且
f(a)=f(b)=0，f’(a)＜0，f’(b)＜0，则方程f’(x)=0在(a，b)内______．
A．没有实根
B．有且仅有一个实根
C．有且仅有两个不等实根
D．至少有两个不等实根
答案
参考答案：D
解析： 利用极限的保号性及f’(a)＜0，f’(b)＜0．先证明存在一点c∈(a，b)，使f(c)=0．于是f(x)有三个零点，两次使用罗尔定理便得到结论D成立．
因
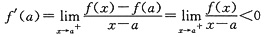，利用极限的保号性，在a的右邻域内必存在点x1，使f(x1)＜0，其中a＜x1＜
．
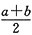同理由f’(b)＜0知，必存在一点x2，使f(x2)＞0，其中
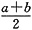＜x2＜b．由连续函数的零点定理知，必存在c∈(x1，x2)
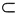(a，b)，使f(c)=0．
在闭区间[a，c]，[c，b]上对f(x)分别使用罗尔定理可知，至少存在一点ξ1∈(a，c)使得f’(ξ1)=0，至少存在一点ξ2∈(c，b)使f’(ξ2)=0．故方程f’(x)=0在(a，b)内至少有两个不等实根，仅D入选．