问题
单项选择题
设A是三阶矩阵，P是三阶可逆矩阵，已知P-1AP=
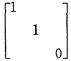，且Aα1=α1，Aα2=α2，Aα3=0，则P是______．
A．[α1，α2，α1+α3]
B．[α2，α3，α1]
C．[2α1+3α2，-8α2，4α3]
D．[α1+α2，α2+α3，α3+α1]
答案
参考答案：C
解析： P的三个列向量是A的对应于特征值的特征向量，判别时要利用下述三条原则：
(1)A的对于同一特征值的特征向量α1，α2的线性组合如kα1，kα1+k2α2仍是A的属于同一特征值的特征向量；
(2)对于不同特征值的特征向量的线性组合(例如其和或其差)不再是A的特征向量；
(3)P中特征向量的排列次序与对角阵中特征值的排列次序一致．利用上述原则即可判定正确的选项．
解一 A．中α1+α3不是A的特征向量，D中α2+α3，α3+α1也不再是A的特征向量，B中特征向量与对角阵中特征值排列不一致，故均不能充当P．仅C入选．
解二 因为α1、α2是λ=1的特征向量，α3是λ=0的特征向量，2α1+3α2，-8α2仍是λ=1的特征向量，4α3仍是λ=0的特征向量，且其排列次序与对角阵中特征值的排列次序一致，仅C入选．