问题
解答题
(理)数列{an}满足a1=1 且8an+1an-16an+1+2an+5=0(n≥1)记bn=
(1)求b1,b2,b3,b4的值. (2)求{bn}、{anbn}的通项公式. (3)求{anbn}的前n项和Sn. |
答案
(1)由bn=
得an=1 an- 1 2
+1 bn
,1 2
代入8an+1an-16an+1+2an+5=0(n≥1),得8(
+1 bn+1
)(1 2
+1 bn
)-16(1 2
+1 bn+1
)+2(1 2
+1 bn
)+5=0,1 2
化简得bn+1=2bn-
,则bn+1-4 3
=2(bn-4 3
),4 3
所以{bn-
}为等比数列,其公比为2,首项为b1-4 3
=4 3
-1 a1- 1 2
=4 3
,2 3
所以bn-
=4 3
•2n-1=2 3
,2n 3
所以bn=
+2n 3
,4 3
所以b1=
+2 3
=2,b2=4 3
+22 3
=4 3
,b3=8 3
+23 3
=4,b4=4 3
+24 3
=4 3
;20 3
(2)由(1)求解过程可知bn=
+2n 3
,4 3
则an=
+1 bn
=1 2
+3 2n+4
,1 2
所以anbn=(
+3 2n+4
)(1 2
+2n 3
)=1+4 3
=2n-1+2 3
+5 3
;2n-1 3
(3)Sn=(
+5 3
)+(1 3
+5 3
)+…+(2 3
+5 3
)=2n-1 3
n+5 3
=
(1-2n)1 3 1-2
n+5 3
.2n-1 3

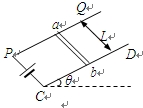
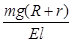 ,水平向右
,水平向右 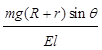 ,垂直于回路平面向下
,垂直于回路平面向下 ,竖直向下
,竖直向下 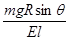 ,垂直于回路平面向下
,垂直于回路平面向下