问题
解答题
已知函数f(x)=
(1)作出f(x)的图象; (2)求f(x)的值域; (3)求f(x)<0时的x取值集合; (4)讨论方程f(x)=b解的个数. |
答案
(1)函数的f(x)=
的图象如下图所示:2x-x2(0<x≤3) x2+6x(-2<x≤0) -
(-∞<x≤-2)4x x+1
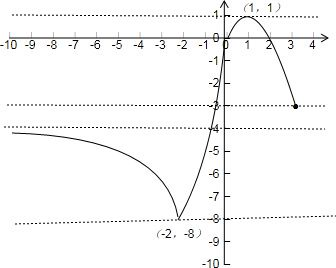
(2)由(1)中函数图象可得:
函数的f(x)=
的值域为:[-8,1]2x-x2(0<x≤3) x2+6x(-2<x≤0) -
(-∞<x≤-2)4x x+1
(3)由(1)中函数图象可得:
当x<0或2<x≤3时,f(x)<0
故f(x)<0时的x取值集合为:(-∞,0)∪(2,3]
(4)当b<-8时,函数图象与直线y=b无交点,此时方程f(x)=b无解;
当b=-8时,函数图象与直线y=b有一个交点,此时方程f(x)=b有一个解;
当-8<b<-4时,函数图象与直线y=b有两个交点,此时方程f(x)=b有两个解;
当b=-4时,函数图象与直线y=b无交点,此时方程f(x)=b无解;
当-4<b<-3时,函数图象与直线y=b有一个交点,此时方程f(x)=b有一个解;
当-3≤b<1时,函数图象与直线y=b有两个交点,此时方程f(x)=b有两个解;
当b=1时,函数图象与直线y=b有一个交点,此时方程f(x)=b有一个解;
当b>1时,函数图象与直线y=b无交点,此时方程f(x)=b无解.
