问题
问答题
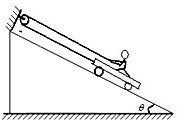
如图所示,在倾角θ=30°的固定斜面上,跨过定滑轮的轻绳一端系在小车的前端,另一端被坐在小车上的人拉住,已知人的质量m=60kg,小车的质量M=10kg,绳及滑轮的质量,滑轮与绳间的摩擦均不计,斜面对小车的摩擦阻力为小车总重的0.1倍,斜面足够长,当人以280N的力拉绳时,求:
(1)人与车一起运动的加速度的大小;
(2)人所受的摩擦力的大小和方向;
(3)某时刻人和车沿斜面向上的速度大小为3m/s,此时人松手,则人和车一起滑到最高点时所用的时间.
答案
(1)将人和车看做整体,受拉力为280×2=560N,总重为(60+10)×10=700N,受阻力为700×0.1=70N,重力平行于斜面的分力为 700×sin30°=350N,
则合外力为F=560-70-350=140N
则根据牛顿第二定律,加速度为a=
=2m/s2140 70
即人与车一起运动的加速度的大小为2m/s2.
(2)人与车有着共同的加速度,所以人的加速度也为2m/s2,对人受力分析,受重力、支持力、拉力和摩擦力,假设静摩擦力沿斜面向上,根据牛顿第二定律,有
ma=T+f-mgsin30°
代入数据解得:f=140N
即人受到沿斜面向上的140N的摩擦力.
(3)失去拉力后,对人和车整体受力分析,受到重力、支持力和沿斜面向下的摩擦力,根据牛顿第二定律,沿斜面的加速度为
a′=
=-6m/s2-350-70 70
根据速度时间公式,有
t=
=0-v0 a′
=0.5s0-3 -6
即人和车一起滑到最高点时所用的时间为0.5s.
